Viiisit [Ruby] - 費波那契數 Successione di Fibonacci！

面試上很常見的費氏數列，來看看如何用 Ruby 的方法來定義吧！

費波那契數 Successione di Fibonacci

在數學上，費波那契數是以遞迴的方法來定義：

F0 = 0; 
F1 = 1; 
Fn = F(n-1) + F(n-2) (n >= 2)

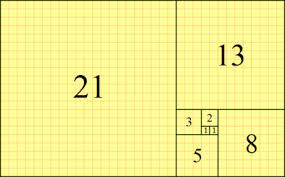
0, 1, 1, 2, 3, 5, 8, 13…
用文字來說，就是費氏數列由0和1開始，之後的費波那契數就是由之前的兩數相加而得出。

遞迴 (Recursive) 是自己呼叫自己的函式，目的是要使用相同的方法，解決重複性的問題。

Remark

遞迴通常用於解決問題的特點是可以被分解為相同結構的子問題，每個子問題都可以使用相同的方法解決。這樣的方法常常以簡單的基本情況為終止條件（例如：設定最小單位），以確保遞迴不會無限運行，也就是說，要用遞迴函式必須確定最小單位是什麼！否則，會發生 stackoverflow 堆疊滿出來的情形!!!

• Method 1

  def fib(n)
    n > 1 ? fib(n-1) + fib(n-2) : n
  end
  
  puts fib(1)
  puts fib(6)
  puts fib(36)

  [Running]
  1
  8
  14930352
  
  [Done] exited with code=0 in 1.072 seconds

  Method 1 使用遞迴方法來計算斐波那契數列。
  計算方式是通過不斷地對 n-1 和 n-2 調用自身來計算第 n 項的斐波那契數。
  這個方法在處理小的 n 值時效率還可以，但對於較大的 n 值，效率會降低，
  因為在計算中多次重複運行相同的子問題，導致指數級的計算時間增長。
  這就是為什麼 Method 1 在處理 n=36 時運行時間較長。

• Method 2

  def fib(n)
    fib_array = [0, 1]
  
    if n < 2
      return fib_array[n]
    end
  
    (2..n).each do |i|
      fib_array[i] = fib_array[i - 1] + fib_array[i - 2]
    end
  
    return fib_array[n]
  end
  
  puts fib(1)
  puts fib(6)
  puts fib(36)

  [Running]
  1
  8
  14930352
  
  [Done] exited with code=0 in 0.059 seconds

Method 2 使用動態方法，在計算過程中避免重複計算，
運用陣列 fib_array 來存已經計算過的斐波那契數值。
Method 2 僅計算一次每個斐波那契數，然後重複使用這些值，因此性能較高。此方法的計算時間是線性，因此不會像 Method 1 那樣出現指數級的計算時間增長。